NumericalAnalysisModule/1 - Numerical Series Approximation

title	author	geometry	output
Análise Numérica - Trabalho Prático 1	Diogo Cordeiro Hugo Sales Pedro Costa	margin=2cm	pdf_document

Motivação

Perceber e analisar técnicas de aproximação de séries numéricas e estratégias para controlo do erro de cálculos em computador, assim como implementar algoritmos com recurso a métodos numéricos adequados e interpretar os resultados.

Questão 1

O eps está definido como a diferença entre 1.0 e o menor valor representável superior a um, por exemplo, 2^-23^, em precisão simples, e 2^-52^ em precisão dupla (em ambos os casos $Base^{-(precisão-1)}$). O ISO 9899 C define:

                   "a diferença entre 1 e o menor valor superior a 1 que é
                       representável num dado tipo de ponto flutuante"

Verificamos a existência de uma definição alternativa: "o menor número que somado com 1 resulta num número maior do que 1". Não usamos esta definição, uma vez que devido ao arredondamento para o valor mais próximo, bastaria usar um valor ligeiramente maior do que metade do nosso eps para satisfazer a condição. E também porque os standards ISO optam por "passo entre valores adjacentes".

O código seguinte implementa o cálculo de

 (2 - \sum _{n=1}^{\infty}\:\frac{1}{2^n}) - 1 = \textit{eps} 

onde

 \lim _{n\to \infty }\sum _{n=1}^{\infty}\:\frac{1}{2^n} = 1^{-} 

Logo este cálculo converge para 1 por números superiores.

\pagebreak

    double machine_eps() {
            // Pela definição, este valor tem que ser superior a 1, e
            // como a máquina usa um sistema de vírgula flutuante de base 2,
            // este tem que ser uma potência de 2
            double epsilon_candidate = 2.0,
                   epsilon = epsilon_candidate,
                   // Primeiro termo da série geométrica com proporção 1/2,
                   // que converge para 1
                   power = 2.0;

            // Diferente de 1 pela definição
            while (epsilon_candidate != 1.0) {
                    epsilon = epsilon_candidate;
                    // Aproximar o epsilon candidate do epsilon,
                    // reduzindo este com a acumulação do termo da sucessão
                    epsilon_candidate -= 1/power;
                    // Razão da sucessão
                    power *= 2;
            }

            return epsilon-1.0;
    }

Com a execução deste código obtivemos 2.2204460492503131e-16, o mesmo valor definido, para aritmética IEEE, na C library float.h.

    #define DBL_EPSILON 2.2204460492503131e-16

Questão 2

Utilizamos o seguinte código na linguagem Java para computar a série dada e obtivemos os resultados apresentados na tabela que segue. Para evitar o cálculo de fatoriais e de grande magnitude, o que diminuiria a performace e aumentaria o erro e a possibilidade de overflow, optamos usar a definição por recorrência e por simplificar algebricamente o cálculo dos termos da série, obtendo uma expressão mais simples.

a_{k+1} = a_k \cdot \frac{k + 1}{4 \cdot k + 6}

    /**
     * Computar a série 2 com um erro absoluto inferior a um dado
     * epsilon
     */
    public static double  compute_series_2(double epsilon) {
            // Fator constante
            double factor = 9.0/(double)(2.0*Math.sqrt(3));
            // Tirado do critério D'Alembert para L = 0.5 < 1
            double super_L = 1.0/(double)(1-0.25);

            // Index do sumatório
            int k = 0;
            // Acumulação do sumatório
            double acc = 0;

            // O valor do termo actual da série
            double a = 1.0f; // a with k = 0
            // Enquanto o nosso erro absoluto é superior ao
            // epsilon dado
            while(epsilon < factor*a*super_L) {
                    // Acumula com o termo anterior
                    acc += a;
                    // Computa o termo seguinte e posteriormente
                    // incrementa k
                    a = compute_serie_2_term(k++) * a;
            }
            System.out.println(factor*acc + " " + (k - 1));
    }

    /**
     * Computa o termo k da série 2 dado um anterior
     */
    public static double compute_serie_2_term(int k) {
            return (double)(k+1.0f)/(double)(4.0f*k+6.0f);
    }

Tabela de resultados

-log(\epsilon)	S_n	Iterações	Tempo (s)
8	3.141592651	13	0.094
9	3.1415926529	14	0.099
10	3.14159265355	16	0.100
11	3.141592653587	18	0.100
12	3.1415926535892	19	0.095
13	3.14159265358976	21	0.101
14	3.141592653589785	22	0.097
15	3.1415926535897936	24	0.097

A série aparenta aproximar o valor de \pi.

Reparamos que geralmente a ordem de grandeza do erro indica o número de casas decimais exatas obtidas, contudo o valor obtido para -log(\epsilon) igual a 9 e 14 produz um resultado com menos uma casa decimal exata. Ainda assim o valor apresentado representa \pi com erro absoluto inferior a 5 \cdot 10^{-10} e 5 \cdot 10^{-15} respetivamente.

Questão 3

Inicialmente implementamos o cálculo do valor aproximado desta série em Java, mas deparamo-nos com um longo tempo de execução devido ao elevado número de iterações necessárias para aproximar a série com o \epsilon pretendido, pelo que decidimos testar uma implementação na linguagem C++, na qual obtivemos maior performace, o que permitiu o cãlculo para um valor menor de \epsilon em tempo útil.

double compute_serie_3_term(unsigned long n) {
       return -((double)(2*n+1))/(double)(2*n+3);
}

void compute_serie_3(double err) {
        // Termo atual
        unsigned long k = 0;
        // Valor do termo atual
        double ak = 1;
        // Acumulador do valor da série
        double acc = 1;
        // Parar quando o erro obtido for inferior ao pretendido
        while (err < 4*std::abs(ak)) {
                // Calcular o termo seguinte e incrementar k
                ak = compute_serie_3_term(k++) * ak;
                // Somar o termo ao total
                acc += ak;
        }

        std::cout << k << " " << 4*acc << '\n';
}

Tabela de Resultados em Java

-log(\epsilon)	S_n	Iterações	Tempo (s)
8	3.141592659	200000000	2.237
9	3.1415926541	2000000000	21.522
10	3.14159265364	20000000012	215.442

Tabela de Resultados em C++

-log(\epsilon)	S_n	Iterações	Tempo (s)
8	3.141592659	200000000	0.787
9	3.1415926541	2000000000	7.862
10	3.14159265364	20000000012	79.130
11	3.141592653593	200000002870	791.625
12	3.1415926535878	2000000614027	7871.842

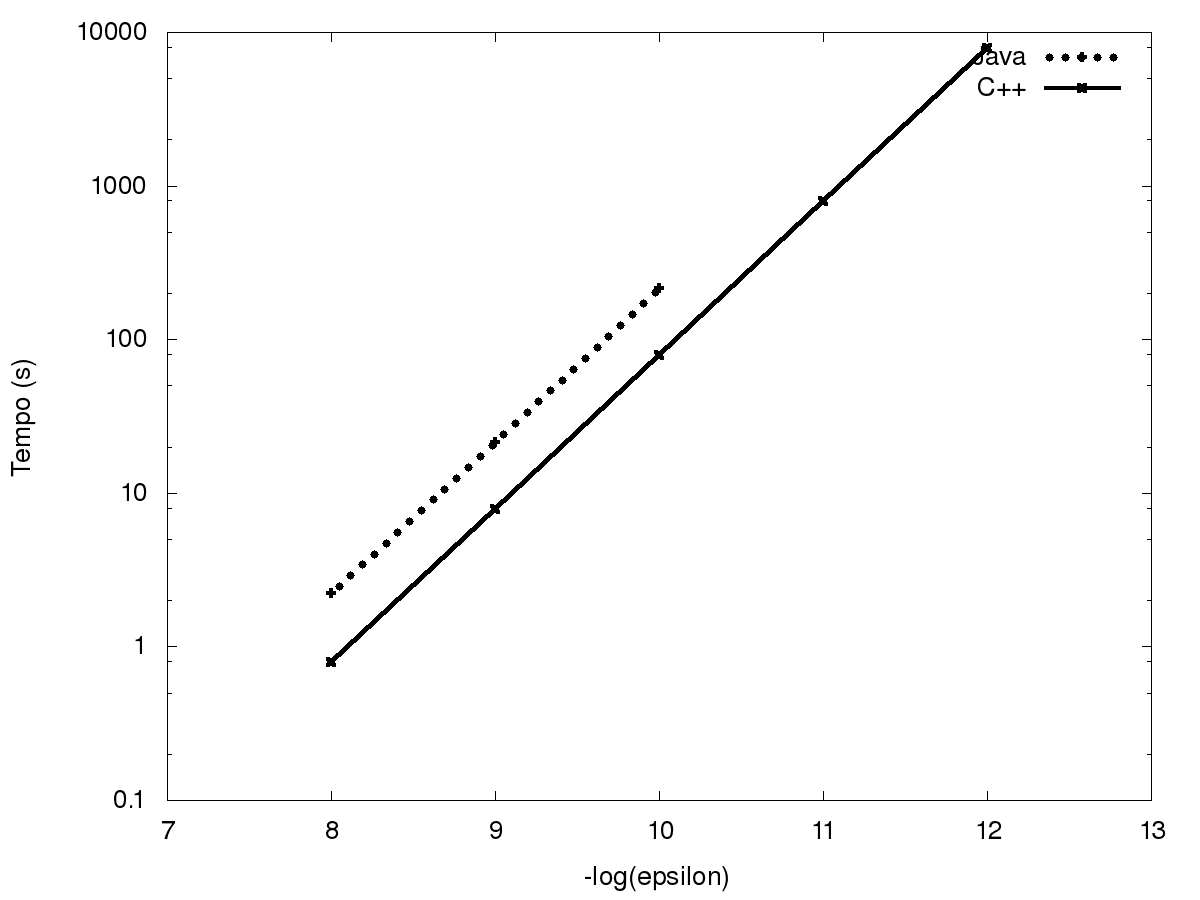
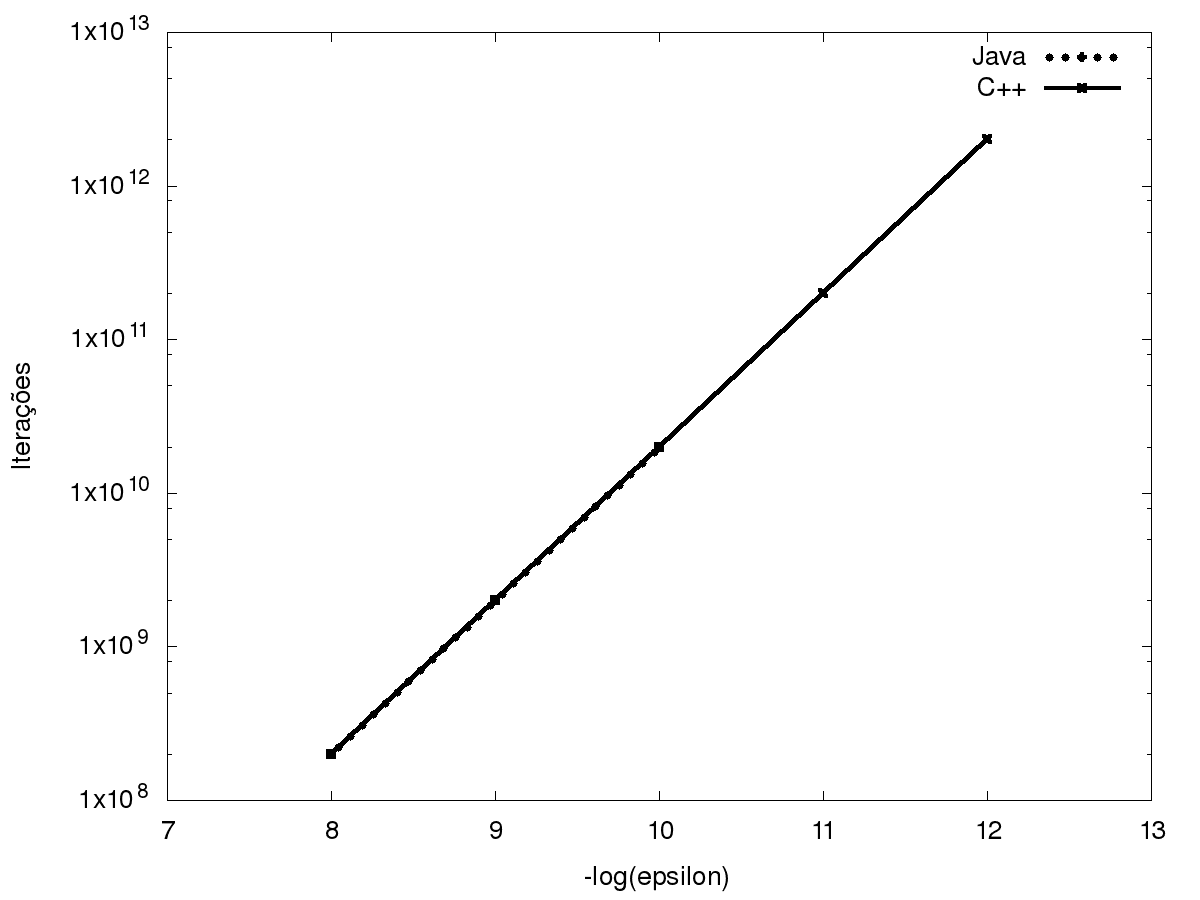
Observando as tabelas notamos um padrão, e, motivados por establecer uma relação entre \epsilon e tanto o números de iterações e o tempo de execução, decidimos traçar um gráfico com estes valores.

{ width=12cm }

{ width=12cm }

\pagebreak

Destes dois gráficos concluímos que o tempo cresce exponencialmente em função do valor de -log(\epsilon), sendo que ambos crescem com um fator de 10, correspondendo aproximadamente a um número da forma 5*10^{-(\epsilon + 1)}, mas não exatamente a este valor, sendo que quando \epsilon diminuiu, o valor de n afasta-se do valor 5*10^{-(\epsilon + 1)}. Descobrimos que se utilizarmos mais precisão nos cálculos (nomeadamente através do uso de long double em C++, ou seja, 128 bits), o padrão verifica-se para todos os casos testados. Concluímos disto que este desvio se deve ao erro de arredondamento ($|S_n - \hat{S}_n|$), que neste caso se deve à elevada magnitude de n.

Questão 4

Usamos como referência

 \pi = 3.14159265358979324

sendo este valor arredondado a 18 algarismos significativos, para que o erro de arredondamento aqui utilizado não altere os resultados do cálculo do erro absoluto efetivo.

Erro efetivo obtido na questão 2:

-log(\epsilon)	\Delta x
8	2.6 \cdot 10^{-09}
9	6.9 \cdot 10^{-10}
10	4.0 \cdot 10^{-11}
11	2.8 \cdot 10^{-12}
12	6.0 \cdot 10^{-13}
13	3.4 \cdot 10^{-14}
14	8.0 \cdot 10^{-15}
15	4.5 \cdot 10^{-16}

Erro efetivo obtido na questão 3:

-log(\epsilon)	\delta x
8	5.5 \cdot 10^{-09}
9	5.2 \cdot 10^{-10}
10	5.1 \cdot 10^{-11}
11	3.3 \cdot 10^{-12}
12	2.0 \cdot 10^{-12}

Notamos que para \epsilon = 10^{-12} o erro efetivamente cometido é maior que o erro pretendido. Justificamos este facto com a elevada magnitude de n, o que leva a termos de pequena magnitude, o que induz erros de cancelamento.

Concluímos que a série utilizada na questão dois possibilita o cálculo da aproximação do valor de \pi usando um número de termos muito menor, para uma mesma precisão. Sendo que a série da questão dois dá resultados com erro inferior a 10^{-15} com um número de iterações na ordem das dezenas, enquanto que a série da questão três requer iterações na ordem das centenas de milhões para obter um erro inferior a 10^{-8}.