NumericalAnalysisModule/3 - Splines

title	author	geometry	output
Análise Numérica - Trabalho Prático 3	Diogo Cordeiro Hugo Sales Pedro Costa	margin=2cm	pdf_document

Motivação

Pretende-se interpolar uma função através do método de Newton em diferenças divididas, construir o spline cúbico natural e proceder a uma comparação e interpretação dos resultados obtidos.

1.a)

using points_t = std::pair<std::vector<double>, std::vector<double>>;
using matrix_t = std::vector<std::vector<double>>;

std::vector<double> newton_differences(points_t points) {
        std::vector<double> factors{};
        auto &[x, fx] = points;
        int n = points.first.size();
        for (int i = 1; i <= n; ++i) {
                factors.push_back(fx[0]);
                for (int j = 0; j < (n - i); ++j) {
                        fx[j] = (fx[j + 1] - fx[j]) / (x[j + i] - x[j]);
                }

        }
        return factors;
}

double newton_polynomial(points_t points, std::vector<double> factors, double x) {
        auto xs = points.first;
        int n = points.second.size() - 1;
        double val = 0;
        for (int k = 0; k <= n; ++k) {
                double acc = 1;
                for(int i = 0; i < k; ++i) {
                        acc *= (x - xs[i]);
                }
                val += acc * factors[k];
        }
        return val;
}

\pagebreak

void exercise_a(points_t points) {
        auto &[xs, fx] = points;
        auto factors = newton_differences(points);
        std::ofstream poly{"a_polynomial.txt"};
        for(double x = 0; x < 4; x += 0.001)
                poly << x << " " << newton_polynomial(points, factors, x) << '\n';

        std::ofstream spline{"a_spline.txt"};
        unsigned long n = xs.size();
        matrix_t mat(n, std::vector<double>(n + 1));
        calculate_natural_cubic_spline_matrix(points, mat);
        for(double x = 0; x < 4; x += 0.001)
                spline << x << " " << natural_cubic_spline(points, mat, x) << '\n';
}

1.b)

void calculate_natural_cubic_spline_matrix(points_t points, matrix_t &mat) {
        auto &[xs, fx] = points;
        int n = xs.size();

        // Construção da matriz
        for (int i = 1; i < n - 1; ++i) {
                mat[i][i - 1] = (xs[i] - xs[i - 1])/6;
                mat[i][i] = (xs[i + 1] - xs[i - 1])/3;
                mat[i][i + 1] = (xs[i + 1] - xs[i])/6;
                mat[i][n] = (fx[i + 1] - fx[i])/(xs[i + 1] - xs[i]) -
                            (fx[i] - fx[i - 1])/(xs[i] - xs[i - 1]);
        }
        mat[0][0] = 1;
        mat[0][n - 1] = 0;
        mat[n - 1][n - 1] = 1;
        mat[n - 1][n] = 0;

        // Passar para a forma triangular
        for (int k = 0; k < n; ++k) {
                for (int i = k + 1; i < n; ++i) {
                        if (mat[k][k] != 0) {
                                double mul = mat[i][k]/mat[k][k];
                                for (int j = k; j < n; ++j) {
                                        mat[i][j] -= mul * mat[k][j];
                                }
                                mat[i][n] -= mul * mat[k][n];
                        }
                }
        }

\pagebreak

        // Resolução da matriz
        for (int i = n - 1; i > 0; --i) {
                if (mat[i][i] != 0) {
                        double mul = mat[i - 1][i]/mat[i][i];
                        for (int j = 0; j < n + 1; ++j) {
                                mat[i - 1][j] -= mul * mat[i][j];
                        }
                        mat[i][n] /= mat[i][i];
                        mat[i][i] = 1;
                }
        }
}

double natural_cubic_spline(points_t points, matrix_t &mat, double x) {

        auto &[xs, fx] = points;
        int n = xs.size();

        int i = 0;
        for (int i_ = 0; i_ < n; ++i_) {
                if (xs[i_] > x){
                        i = i_;
                        break;
                }
        }

        double hi = xs[i] - xs[i - 1];
        return mat[i - 1][n] * std::pow((xs[i] - x), 3)/(6 * hi) +
               mat[i][n] * std::pow((x - xs[i - 1]), 3)/(6 * hi) +
               (fx[i - 1] - mat[i - 1][n] * (hi * hi)/6)*(xs[i] - x)/hi +
               (fx[i] - mat[i][n] * (hi * hi)/6)*(x - xs[i - 1])/hi;

}

void exercise_b() {
        points_t points;
        auto &[xs, fx] = points;
        auto f = [](double x) { return 4 * std::pow(x, 2) + std::sin(9 * x); };

        for (double x = -1; x <= 1; x += (1 - -1)/8.0) {
                xs.push_back(x);
                fx.push_back(f(x));
        }

        std::ofstream poly{"b_polynomial.txt"};
        auto factors = newton_differences(points);
        for(double x = -1; x < 1; x += 0.001)
                poly << x << " " << newton_polynomial(points, factors, x) << '\n';

        std::ofstream spline{"b_spline.txt"};
        unsigned long n = xs.size();
        matrix_t mat(n, std::vector<double>(n + 1));
        calculate_natural_cubic_spline_matrix(points, mat);
        for(double x = -1; x < 1; x += 0.001)
                spline << x << " " << natural_cubic_spline(points, mat, x) << '\n';
}

2.a)

{ width=10cm }

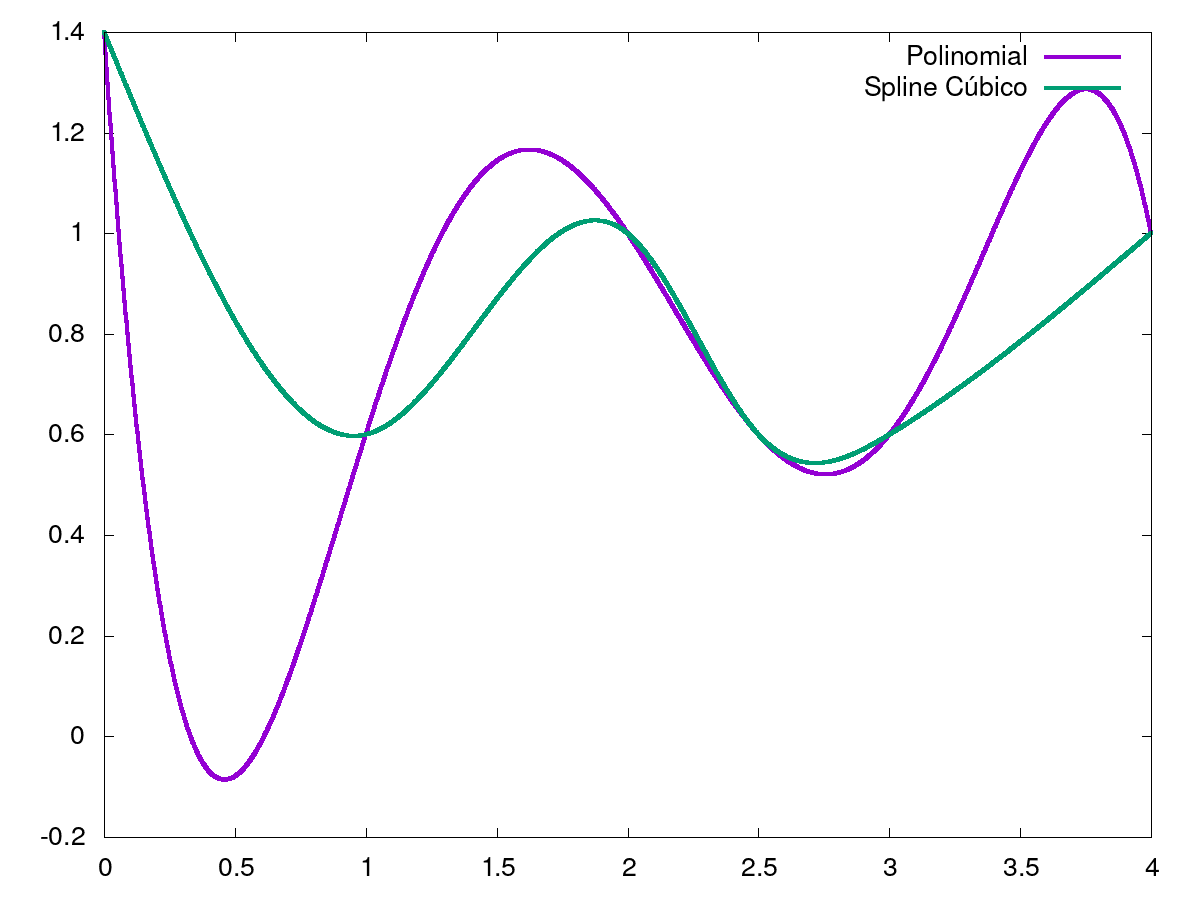
Através dos graficos é possivel verificar que os valores das funções coincidem no pontos de interpolação, como era esperado. Não é possivel determinal qual a melhor aproximação sem conhecer a função original. O programa foi modificado para imprimir a matriz inicial assim como o resultado final, que foi utilizado para calcular o vetor resíduo e a norma deste. Este script encontra-se em baixo.

#!/usr/bin/env python3

import numpy as np
from scipy.linalg import solve
from numpy.linalg import norm

# Matriz construída pelo programa em C++
A = np.matrix([[1,        0,        0,         0,         0,         0],
               [0.166667, 0.666667, 0.166667,  0,         0,         0],
               [0,        0.166667, 0.5,       0.0833333, 0,         0],
               [0,        0,        0.0833333, 0.333333,  0.0833333, 0],
               [0,        0,        0,         0.0833333, 0.5,       0.166667],
               [0,        0,        0,         0,         0,         1]])

b = np.array([0, 1.2, -1.2, 0.8, 0.4, 0])

x2 = np.array([0, 2.76846, -3.87386, 3.30622, 0.248963, 0])

x = solve(A, b)

print(norm(x - x2))

Obteu-se para a norma do vetor resíduo o valor 1.0e-05 que é considerado aceitável visto que os dados são apresentados com dois algarismos significativos.

\pagebreak

2.b)

i)

\begin{array}{c|ccccccccc}{x_{i}} & {-1} & {-0.75} & {-0.5} & {-0.25} & {0} &
{0.25} & {0.5} & {0.75} & {1} \\ \hline {f_{i}} & {3.58788} & {1.79996} &
{1.97753} & {-0.528073} & {0} & {1.02807} & {0.0224699} & {2.70004} & {4.41212}
\end{array}

ii)

{ width=10cm }

De forma análoga ao exercício 2.a) foi calculada a norma do vetor resíduo usando o seguinte script:

A = np.matrix(
[[1,         0,         0,         0,         0,         0,         0,         0,         0],
 [0.0416667, 0.166667,  0.0416667, 0,         0,         0,         0,         0,         0],
 [0,         0.0416667, 0.166667,  0.0416667, 0,         0,         0,         0,         0],
 [0,         0,         0.0416667, 0.166667,  0.0416667, 0,         0,         0,         0],
 [0,         0,         0,         0.0416667, 0.166667,  0.0416667, 0,         0,         0],
 [0,         0,         0,         0,         0.0416667, 0.166667,  0.0416667, 0,         0],
 [0,         0,         0,         0,         0,         0.0416667, 0.166667,  0.0416667, 0],
 [0,         0,         0,         0,         0,         0,         0.0416667, 0.166667,  0.0416667],
 [0,         0,         0,         0,         0,         0,         0,         0,         1]])

b = np.array([0, 7.862, -10.7327, 12.1347, 2, -8.13471, 14.7327, -3.862, 0])

x2 = np.array([0, 73.9996, -107.31, 97.6564, 7.91753, -81.3265, 122.156, -53.7109, 0])

x = solve(A, b)

print(norm(x - x2))

Obteu-se para a norma do vetor resíduo o valor 9.0e-04 que é considerado aceitável visto que este valor tem uma magnitude pequena.

\pagebreak

iii)

x	f(x)	p(x)	abs(f(x)-p(x))	s(x)	f(x)-s(x)
0.30	0.78737988	0.923318	1.4*10^{-1}	0.826621	4.0*10^{-2}
0.83	3.68278040	4.834190	1.2	2.4*10^{-1}	2.4*10^{-1}

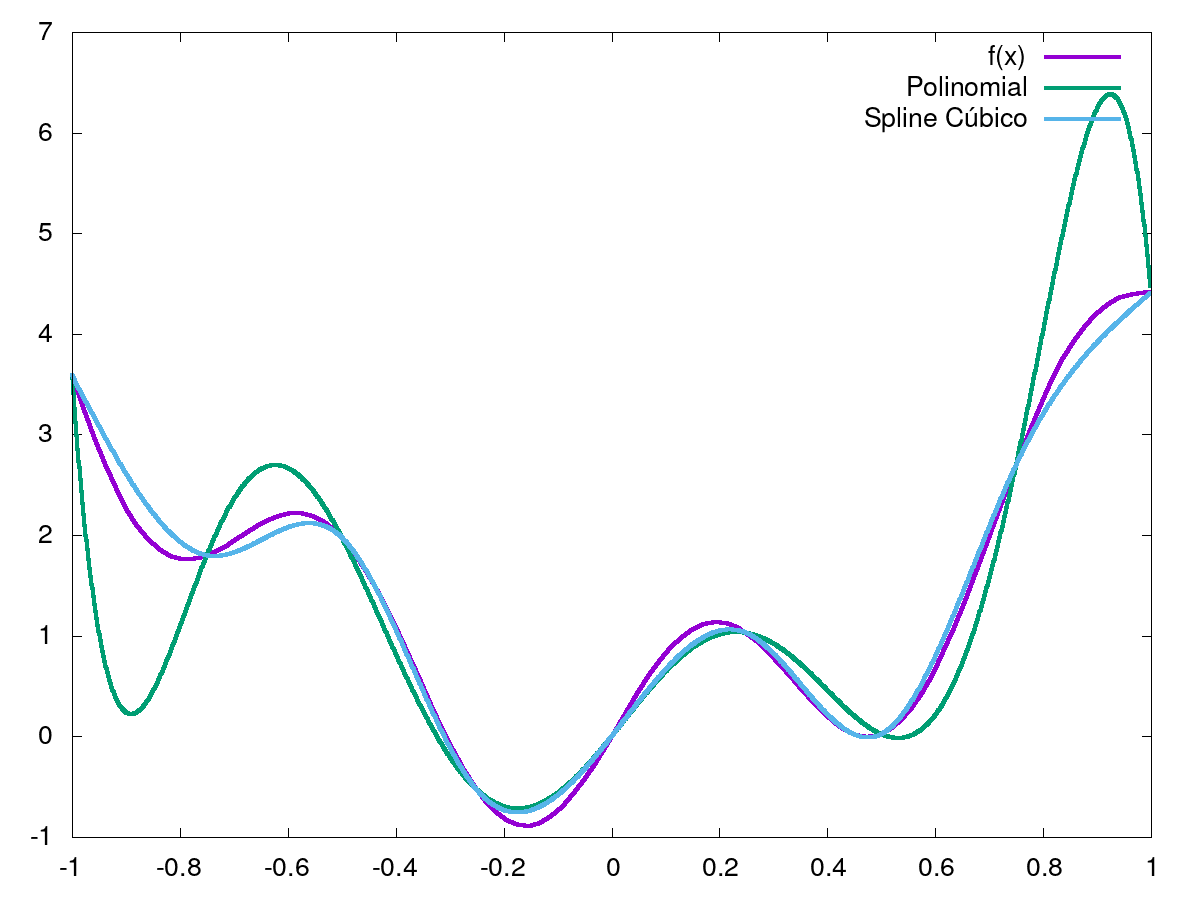
Verificamos que o erro do spline cubico é inferior em ambos os casos. Além disso em ambos os casos o erro é maior quando a abcissa é mais distante do centro do intervalo.

iv)

É possivel observar que a interpolação pelo spline aproxima, em geral, melhor a função dada do que o polinomio. Em particular verifica-se que o erro do polinomio acentua-se à medida que as abcissas se afastam do centro do intervalo de interpolação.