Introduction
The Prolog Factor Language (PFL) is a language that extends Prolog for providing a syntax to describe first-order probabilistic graphical models. These models can be either directed (bayesian networks) or undirected (markov networks). This language replaces the old one known as CLP(BN).The package also includes implementations for a set of well-known inference algorithms for solving probabilistic queries on these models. Both ground and lifted inference methods are support.
Installation
PFL is included with the YAP Prolog system. However, there isn't yet a stable release of YAP that includes PFL and you will need to install a development version. To do so, you must have installed the Git version control system. The commands to perform a default installation of YAP in your home directory in a Unix-based environment are shown next.
$ cd $HOME
$ git clone git://yap.git.sourceforge.net/gitroot/yap/yap-6.3
$ cd yap-6.3/
$ ./configure --enable-clpbn-bp --prefix=$HOME
$ make depend & make install
In case you want to install YAP somewhere else or with different settings, please consult the YAP documentation. From now on, we will assume that the directory $HOME ▷ bin (where the binary is) is in your $PATH environment variable.
Once in a while, we will refer to the PFL examples directory. In a default installation, this directory will be located at $HOME ▷ share ▷ doc ▷ Yap ▷ packages ▷ examples ▷ CLPBN.
Language
A first-order probabilistic graphical model is described using parametric factors, commonly known as parfactors. The PFL syntax for a parfactor isType F ; Phi ; C.
-
Type refers the type of network over which the parfactor is defined. It can be bayes for directed networks, or markov for undirected ones.
-
F is a comma-separated sequence of Prolog terms that will define sets of random variables under the constraint C. If Type is bayes, the first term defines the node while the remaining terms define its parents.
-
Phi is either a Prolog list of potential values or a Prolog goal that unifies with one. Notice that if Type is bayes, this will correspond to the conditional probability table. Domain combinations are implicitly assumed in ascending order, with the first term being the 'most significant' (e.g.
x0y0,
x0y1,
x0y2,
x1y0,
x1y1,
x1y2).
- C is a (possibly empty) list of Prolog goals that will instantiate the logical variables that appear in F, that is, the successful substitutions for the goals in C will be the valid values for the logical variables. This allows the constraint to be defined as any relation (set of tuples) over the logical variables.
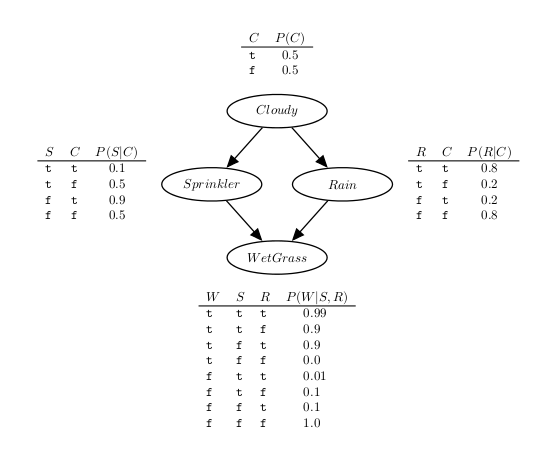
Towards a better understanding of the language, next we show the PFL representation for the sprinkler network found in the above figure.
:- use_module(library(pfl)).
bayes cloudy ; cloudy_table ; [].
bayes sprinkler, cloudy ; sprinkler_table ; [].
bayes rain, cloudy ; rain_table ; [].
bayes wet_grass, sprinkler, rain ; wet_grass_table ; [].
cloudy_table(
[ 0.5,
0.5 ]).
sprinkler_table(
[ 0.1, 0.5,
0.9, 0.5 ]).
rain_table(
[ 0.8, 0.2,
0.2, 0.8 ]).
wet_grass_table(
[ 0.99, 0.9, 0.9, 0.0,
0.01, 0.1, 0.1, 1.0 ]).
In the example, we started by loading the PFL library, then we have defined one factor for each node, and finally we have specified the probabilities for each conditional probability table.
Notice that this network is fully grounded, as all constraints are empty. Next we present the PFL representation for a well-known markov logic network - the social network model. For convenience, the two main weighted formulas of this model are shown below.
1.5 : Smokes(x) => Cancer(x) 1.1 : Smokes(x) ^ Friends(x,y) => Smokes(y)
Next, we show the PFL representation for this model.
:- use_module(library(pfl)).
person(anna).
person(bob).
markov smokes(X), cancer(X) ;
[4.482, 4.482, 1.0, 4.482] ;
[person(X)].
markov friends(X,Y), smokes(X), smokes(Y) ;
[3.004, 3.004, 3.004, 3.004, 3.004, 1.0, 1.0, 3.004] ;
[person(X), person(Y)].
Notice that we have defined the world to be consisted of only two persons, anna and bob. We can easily add as many persons as we want by inserting in the program a fact like person @ 10. . This would automatically create ten persons named p1, p2, ..., p10.
Unlike other fist-order probabilistic languages, in PFL the logical variables that appear in the terms are not directly typed, and they will be only constrained by the goals that appears in the constraint of the parfactor. This allows the logical variables to be constrained to any relation (set of tuples), and not only pairwise (in)equalities. For instance, the next example defines a network with three ground factors, each defined respectively over the random variables p(a,b), p(b,d) and p(d,e).
constraint(a,b). constraint(b,d). constraint(d,e). markov p(A,B); some_table; [constraint(A,B)].
We can easily add static evidence to PFL programs by inserting a fact with the same functor and arguments as the random variable, plus one extra argument with the observed state or value. For instance, suppose that we know that anna and bob are friends. We can add this knowledge to the program with the following fact: friends(anna,bob,t). .
One last note for the domain of the random variables. By default, all terms instantiate boolean (t/f) random variables. It is possible to choose a different domain for a term by appending a list of its possible values or states. Next we present a self-explanatory example of how this can be done.
bayes professor_ability::[high, medium, low] ; [0.5, 0.4, 0.1].
More probabilistic models defined using PFL can be found in the examples directory.
Querying
In this section we demonstrate how to use PFL to solve probabilistic queries. We will use the sprinkler network as example.Assuming that the current directory is the one where the examples are located, first we load the model with the following command.
$ yap -l sprinkler.pfl
Let's suppose that we want to estimate the marginal probability for the WetGrass random variable. To do so, we call the following goal.
?- wet_grass(X).
The output of this goal will show the marginal probability for each WetGrass possible state or value, that is, t and f. Notice that in PFL a random variable is identified by a term with the same functor and arguments plus one extra argument.
Now let's suppose that we want to estimate the probability for the same random variable, but this time we have evidence that it had rained in the day before. We can estimate this probability without resorting to static evidence with:
?- wet_grass(X), rain(t).
PFL also supports calculating joint probability distributions. For instance, we can obtain the joint probability for Sprinkler and Rain with:
?- sprinkler(X), rain(Y).
Options
PFL supports both ground and lifted inference methods. The inference algorithm can be chosen by calling set_solver/1. The following are supported:- ve, variable elimination (written in Prolog)
- hve, variable elimination (written in C++)
- jt, junction tree
- bdd, binary decision diagrams
- bp, belief propagation
- cbp, counting belief propagation
- gibbs, gibbs sampling
- lve, generalized counting first-order variable elimination (GC-FOVE)
- lkc, lifted first-order knowledge compilation
- lbp, lifted first-order belief propagation
For instance, if we want to use belief propagation to solve some probabilistic query, we need to call first:
?- set_solver(bp).
It is possible to tweak some parameters of PFL through set_pfl_flag/2 predicate. The first argument is a option name that identifies the parameter that we want to tweak. The second argument is some possible value for this option. Next we explain the available options in detail.
verbosity
This option controls the level of debugging information that will be shown.- Values: a positive integer (default is 0 - no debugging). The higher the number, the more information that will be shown.
- Affects: hve, bp, cbp, lve, lkc and lbp.
For instance, we can view some basic debugging information by calling the following goal.
?- set_pfl_flag(verbosity, 1).
use_logarithms
This option controls whether the calculations performed during inference should be done in a logarithm domain or not.- Values: true (default) or false.
- Affects: hve, bp, cbp, lve, lkc and lbp.
hve_elim_heuristic
This option allows to choose which elimination heuristic will be used by the hve.- Values: sequential, min_neighbors, min_weight, min_fill and
weighted_min_fill (default). - Affects: hve.
An explanation for each of these heuristics can be found in Daphne Koller's book Probabilistic Graphical Models.
bp_max_iter
This option establishes a maximum number of iterations. One iteration consists in sending all possible messages.- Values: a positive integer (default is 1000).
- Affects: bp, cbp and lbp.
bp_accuracy
This option allows to control when the message passing should cease. Be the residual of one message the difference (according some metric) between the one sent in the current iteration and the one sent in the previous. If the highest residual is lesser than the given value, the message passing is stopped and the probabilities are calculated using the last messages that were sent.- Values: a float-point number (default is 0.0001).
- Affects: bp, cbp and lbp.
bp_msg_schedule
This option allows to control the message sending order.- Values:
- seq_fixed (default), at each iteration, all messages are sent with the same order.
- seq_random, at each iteration, all messages are sent with a random order.
- parallel, at each iteration, all messages are calculated using only the values of the previous iteration.
- max_residual, the next message to be sent is the one with maximum residual (as explained in the paper Residual Belief Propagation: Informed Scheduling for Asynchronous Message Passing).
- Affects: bp, cbp and lbp.
export_libdai
This option allows exporting the current model to the libDAI file format.- Values: true or false (default).
- Affects: hve, bp, and cbp.
export_uai
This option allows exporting the current model to the UAI file format.- Values: true or false (default).
- Affects: hve, bp, and cbp.
export_graphviz
This option allows exporting the factor graph's structure into a format that can be parsed by Graphviz.- Values: true or false (default).
- Affects: hve, bp, and cbp.
print_fg
This option allows to print a textual representation of the factor graph.- Values: true or false (default).
- Affects: hve, bp, and cbp.
Learning
PFL is capable to learn the parameters for bayesian networks, through an implementation of the expectation-maximization algorithm.Next we show an example of parameter learning for the sprinkler network.
:- [sprinkler.pfl].
:- use_module(library(clpbn/learning/em)).
data(t, t, t, t).
data(_, t, _, t).
data(t, t, f, f).
data(t, t, f, t).
data(t, _, _, t).
data(t, f, t, t).
data(t, t, f, t).
data(t, _, f, f).
data(t, t, f, f).
data(f, f, t, t).
main :-
findall(X, scan_data(X), L),
em(L, 0.01, 10, CPTs, LogLik),
writeln(LogLik:CPTs).
scan_data([cloudy(C), sprinkler(S), rain(R), wet_grass(W)]) :-
data(C, S, R, W).
Parameter learning is done by calling the em/5 predicate. Its arguments are the following.
em(+Data, +MaxError, +MaxIters, -CPTs, -LogLik)
- Data is a list of samples for the distribution that we want to estimate. Each sample is a list of either observed random variables or unobserved random variables (denoted when its state or value is not instantiated).
- MaxError is the maximum error allowed before stopping the EM loop.
- MaxIters is the maximum number of iterations for the EM loop.
- CPTs is a list with the estimated conditional probability tables.
- LogLik is the log-likelihood.
It is possible to choose the solver that will be used for the inference part during parameter learning with the set_em_solver/1 predicate (defaults to hve). At the moment, only the following solvers support parameter learning: ve, hve, bdd, bp and cbp.
Inside the learning directory from the examples directory, one can find more examples of parameter learning.
External Interface
This package also includes an external command for perform inference over probabilistic graphical models described in formats other than PFL. Currently two are support, the http://cs.ru.nl/ jorism/libDAI/doc/fileformats.htmllibDAI file format, and the http://graphmod.ics.uci.edu/uai08/FileFormatUAI08 file format.This command's name is hcli and its usage is as follows.
$ ./hcli [solver=hve|bp|cbp] [<OPTION>=<VALUE>]... <FILE>[<VAR>|<VAR>=<EVIDENCE>]...
Let's assume that the current directory is the one where the examples are located. We can perform inference in any supported model by passing the file name where the model is defined as argument. Next, we show how to load a model with hcli.
$ ./hcli burglary-alarm.uai
With the above command, the program will load the model and print the marginal probabilities for all defined random variables. We can view only the marginal probability for some variable with a identifier X, if we pass X as an extra argument following the file name. For instance, the following command will output only the marginal probability for the variable with identifier 0.
$ ./hcli burglary-alarm.uai 0
If we give more than one variable identifier as argument, the program will output the joint probability for all the passed variables.
Evidence can be given as a pair containing a variable identifier and its observed state (index), separated by a '=`. For instance, we can introduce knowledge that some variable with identifier 0 has evidence on its second state as follows.
$ ./hcli burglary-alarm.uai 0=1
By default, all probability tasks are resolved using the hve solver. It is possible to choose another solver using the solver option as follows.
$ ./hcli solver=bp burglary-alarm.uai
Notice that only the hve, bp and cbp solvers can be used with hcli.
The options that are available with the set_pfl_flag/2 predicate can be used in hcli too. The syntax is a pair <Option>=<Value> before the model's file name.
Papers
- Evaluating Inference Algorithms for the Prolog Factor Language.