6.0 KiB
Executable File
class: title, smokescreen, shelf, no-footer
Análise Numérica - Trabalho Prático 4
Diogo Cordeiro, Hugo Sales, Pedro Costa, Ricardo Pimenta
class: roomy
Motivação
Pretende-se compreender o funcionamento conceptual bem como os desafios da implementação de dois métodos numéricos: Regra de Simpson e Regra dos Trapézios.
class: img-right
1
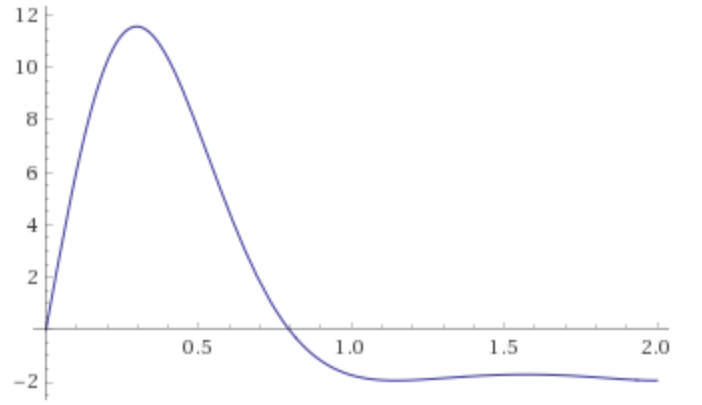
Através da análise do gráfico, verificamos que o majorante, em valor absoluto, da 4ª derivada da função é menor que 12, este valor é usado para majorar a formula do erro para o calculo de n.
class: compact
Simpson
Função que implementa o método de Simpson
double simpson (Function f, double a, double b, int n)
{
// Intervalo de passo
double h = (b - a)/n;
// Valor de f nos pontos de indice par
double evens = summation(f, 2, n - 2, 2, h, a);
// Valor de f nos pontos de indice impar
double odds = summation(f, 1, n - 1, 2, h, a);
// Aplicação da método de Simpson
value = (h/3)*(f(a) + f(b) + 2 * evens + 4 * odds);
}
class: compact
Summation
Função para calcular o sumatório de F entre os pontos de indice init e stop saltando step pontos, usando h como intervalo de passo
double summation (Function f, int init, int stop, int step, double h, double a)
{
// Acumulador
double total = 0;
for (int i = init; i <= stop; i += step) {
// Adicionamos o valor de f correspondente ao x de indice i
total += f(a + i * h);
}
return total;
}
class: compact
calculateN
Função para calcular o número de pontos necessários para o calculo do integral com erro menor que error
int calculateN (double A, double B, double error) {
int n = ceil( (B - A) / pow((15.0 * error) / 2.0, 1.0 / 4) );
return n + (n % 2);
}
class: compact
main
void main ()
{
Function f(x) = sin(sin(sin(sin(x))));
// com 7 casas decimais correctas
print(simpson(f, 0, 2, calculateN(0, 2, pow(10, -7))));
// com 12 casas decimais correctas
print(simpson(f, 0, 2, calculateN(0, 2, pow(10, -12))));
}
class: roomy
<style> table td { background: inherit; border-radius: .5em; color: #000; } </style>Output
| Erro | Resultado |
|---|---|
10^{-7} |
1.0548418906594816 |
10^{-12} |
1.0548418772492483 |
class: compact
2)
// Valor exacto do integral calculado com o WolframAlpha, arredondado
// com 15 algarismos significativos, um a mais do que o erro majorado
// máximo para o caso de 2^20 pontos.
double I = 1.05484187724912;
/* Função para calcular o integral recorrendo ao método do Trapézio */
double trapezio (Function f, double a, double b) {
// Acumulador
double summation = 0;
// Intervalo de passo com n inicial = 2
double h = (b - a)/2;
// Valor constante
double fa_fb = f(a) + f(b);
class: compact
2)
// Para cada expoente de 1 a 20 (com passo 1)
for (int k = 1; k <= 20; ++k) {
// Guarda sumatorio dos pontos anteriores
double partial_sum = 0;
// Número de intervalos
// Com o left shift fazemos a potência de 2^k
int n = 1 << k;
// Evitamos recalcular pontos da função previamente computados
// guardando o sumatório destes em partial_sum e adicionamos a cada
// iteração os pontos novos, sendo estes de indice impar
for (int i = 1; i < n; i += 2) {
// Adicionamos o valor de f correspondente ao x de indice i
partial_sum += f(a + i * h);
}
summation += partial_sum;
class: compact
2)
// Aplicação da formula do Trapézio
double value = (h/2)*fa_fb + h * summation;
print(k + "\t| " + value + "\t| " + (I - value));
// Dividimos o intervalo por 2
h /= 2;
}
}
void main () {
Function f(x) = sin(sin(sin(sin(x))));
print(trapezio(f, 0, 2);
}
class: compact
<style> table td { background: inherit; border-radius: .5em; color: #000; } </style>Output
| k | I_{n_{k}} |
\mid I - I_{n_{k}} \mid |
|---|---|---|
| 1 | 0.9533749638740736 | 1.1 \cdot 10^{-1} |
| 2 | 1.0308378382617962 | 2.5 \cdot 10^{-2} |
| 3 | 1.0489039934457873 | 6.0 \cdot 10^{-3} |
| 4 | 1.053360809734676 | 1.5 \cdot 10^{-3} |
| 5 | 1.0544718169560368 | 3.8 \cdot 10^{-4} |
| 6 | 1.054749374997165 | 9.3 \cdot 10^{-5} |
| 7 | 1.0548187524860693 | 2.4 \cdot 10^{-5} |
class: compact
<style> table td { background: inherit; border-radius: .5em; color: #000; } </style>Output
| k | I_{n_{k}} |
\mid I - I_{n_{k}} \mid |
|---|---|---|
| 8 | 1.0548360961083287 | 5.8 \cdot 10^{-6} |
| 9 | 1.054840431967042 | 1.5 \cdot 10^{-6} |
| 10 | 1.0548415159287925 | 3.6 \cdot 10^{-7} |
| 11 | 1.0548417869190467 | 9.1 \cdot 10^{-8} |
| 12 | 1.0548418546666 | 2.3 \cdot 10^{-8} |
| 13 | 1.054841871603487 | 5.7 \cdot 10^{-9} |
| 14 | 1.0548418758377078 | 1.5 \cdot 10^{-9} |
class: compact
<style> table td { background: inherit; border-radius: .5em; color: #000; } </style>Output
| k | I_{n_{k}} |
\mid I - I_{n_{k}} \mid |
|---|---|---|
| 15 | 1.0548418768962615 | 3.5 \cdot 10^{-10} |
| 16 | 1.0548418771608998 | 8.9 \cdot 10^{-11} |
| 17 | 1.0548418772270582 | 2.3 \cdot 10^{-11} |
| 18 | 1.0548418772436017 | 5.6 \cdot 10^{-12} |
| 19 | 1.0548418772477444 | 1.4 \cdot 10^{-12} |
| 20 | 1.0548418772487873 | 3.3 \cdot 10^{-13} |