7.4 KiB
class: title, smokescreen, shelf, no-footer
Análise Numérica - Trabalho Prático 1
Diogo Cordeiro | Hugo Sales | Pedro Costa | Ricardo Pimenta
name: motivacao class: roomy
Motivação
Pretende-se usar os métodos de Newton e iterativo simples para determinar um valor aproximado de um zero de
x^2 - cos(x)^2name: 1a class: compact
1.a)
Optamos por implementar o algoritmo pedido em C++ devido à possiblidade da aplicação de templates e lambdas. Deste modo, foi-nos possível implementar os dois métodos pedidos partindo de um algoritmo genérico pois a diferença entre o método de Newton e o método iterativo consiste apenas na fórmula de recorrência. Assim, o método de Newton pode ser visto como uma forma do método iterativo simples.
int main() {
auto F = [](double x){ return std::pow(x, 2.0) - std::pow(std::cos(x), 2.0); };
auto dF = [](double x){ return 2.0 * x + std::sin(2.0 * x); };
double epsilon = 5.0 * std::pow(10.0, -12.0);
std::cout << newton(0.8, epsilon, F, dF, 100000) << `\n`;
}
name: 1a class: compact
1.a)
template<typename step_func>
double find_root(double x0, double epsilon, step_func step, long iter_limit) {
double x1 = x0, err;
long iter = 1;
do {
x0 = x1;
x1 = step(x0);
err = std::abs(x1 - x0);
} while(err > epsilon && iter++ < iter_limit);
return x1;
}
template<typename F_t, typename dF_t>
double newton(double x0, double epsilon, F_t F, dF_t dF, long iter_limit) {
return find_root(x0, epsilon,
[&F, &dF](double x0){ return x0 - F(x0)/dF(x0); },
iter_limit);
}
name: 1b class: compact, img-right
1.b)
![Gráfico para \(x \in [-1;1]\)](/diogo/NumericalAnalysisModule/media/commit/b7b704b68ba63d7958927ddd9b5bef232573f8d9/2%20-%20Newton%20and%20Iterative%20methods/slides/graph.png)
Como \(\forall{x}: cos^2(x) \in [0:1]\), temos que \(x^2 \geq cos^2(x)\) para \(|x| > 1\), sabemos que o comportamento de \(f(x)\) é dominado pelo comportamento de \(x^2\), a qual só tem duas raízes.
A menor das raízes encontra-se no intervalo \(]-\infty;0]\) e a maior destas em \([0;\infty[\).
name: 1b-cont class: compact, img-right
1.b)
![Gráfico para \(x \in [0.7;0.8]\)](/diogo/NumericalAnalysisModule/media/commit/b7b704b68ba63d7958927ddd9b5bef232573f8d9/2%20-%20Newton%20and%20Iterative%20methods/slides/graph_small.png)
Através da análise do gráfico, verificamos que o intervalo \([0.7;0.8]\) contém uma raíz. Definimos então \(a = 0.7\) e \(b = 0.8\).
name: 1c class: compact
1.c)
Queremos mostrar que as condições de aplicabilidade do método de Newton são satisfeitas no intervalo. Assim,
F(x) = x^2 - cos(x)^2F'(x) = 2 \cdot x + sin(2 \cdot x)F''(x) = 2 + 2 \cdot cos(2 \cdot x)Como todas estas funções são compostas partindo de somas de funções contínuas em \(\mathbb{R}\), são também continuas no intervalo considerado, verificando-se assim o primeiro critério.
Dado que,
F(a) < 0, F(b) < 0 \Rightarrow F(a) \cdot F(b) < 0name: 1c-cont class: compact
1.c)
Verifica-se também o segundo critério.
Temos que \(F''(x) = 2 + 2 \cdot cos(2 \cdot x)\), logo \(cos(2 \cdot x) \in [-1;1]\), por isso \(2 \cdot cos(2 \cdot x) \in [-2; 2]\), e \(2 \cdot cos(2 \cdot x) + 2 \in [0;4]\) o que implica que \(F''(x) \geq 0\), para \(x \in \mathbb{R}\) e por isso \(F'(x)\) é não decrescente em \(\mathbb{R}\), ou seja, \(F'(b) \geq F'(a)\) e \(F'(a) > 3\) e por isso \(F'(x) \neq 0 \forall{x} : \in [a;b]\), o que verifica o terceiro critério.
Como foi dito anteriormente, \(F''(x) \geq 0\) em \(\mathbb{R}\) e, por isso, também para \(\forall{x} : \in [a;b]\), verificando-se a quarta condição.
Para \(x_0 = b\), temos que \(F(x_0) > 0\) e \(F''(x_0) > 0\), logo \(F(x_0) \cdot F''(x_0) > 0\), verificando-se a quinta condição.
Então a sucessão gerada converge para a unica raíz no intervalo \([a;b]\).
name: 1d class: compact
1.d)
Aplicamos o programa apresentado em \(1.a\) e obtivemos os seguintes resultados.
| Iterações | Erro estimado | Valor |
|---|---|---|
| 1 | 5.9e-02 | 0.740528800196 |
| 2 | 1.4e-03 | 0.739086050826 |
| 3 | 9.2e-07 | 0.739085133216 |
| 4 | 3.7e-13 | 0.739085133215 |
Verficamos que o erro estimado é aproximadamente metade do erro estimado da iteração amterior, o que justificamos com o facto de que o resultado teórico nos dizer que o erro converge segundo uma secessão de segunda ordem.
name: 1e class: compact
1.e)
Aplicando a fórmula
\( M = \frac{1}{2} \cdot \frac{\max \limits_{a \leq x \leq b} | F''(x) | }{\min \limits_{a \leq x \leq b} | F'(x) | } \)Como \(F''(x)\) é decrescente em \([0;\pi/2]\), então \(\max\limits_{a \leq x \leq b} | F''(x) | = |F''(a)|\) e como \(F'(x)\) é não decrescente em \(\mathbb{R}\), \(\min\limits_{a \leq x \leq b} | F'(x) | = F'(a)\).
Assim, obtemos \(M = \frac{F''(0.7)}{2F'(0.7)} \leq \frac{2.4}{2 \cdot 2.3} \leq 0.53\) e
\(n \geq \frac{ln(\alpha)}{ln(2)}, \alpha = \frac{ln(5 \cdot 10^{-14}) + ln(0.53)}{ln(0.53) + ln(10^{-1})}\), logo \(\alpha \leq \frac{-32}{2.9} \leq 12\) e \(n \geq 4\), ou seja que com 4 iterações conseguimos um erro absoluto inferior a \(5 \cdot 10^{-14}\).
name: 2a class: compact
2.a)
Dada a implementação genérica do algoritmo, o método iterativo simples pode ser implementado sucintamente como:
template<typename F_t>
double fixed_point(double x0, double epsilon, F_t f, long iter_limit) {
return find_root(x0, epsilon, f, iter_limit);
}
name: 2a-cont class: compact
2.a)
e usado como
auto f = [](double x){ return std::cos(x); };
std::cout << fixed_point(0.8, epsilon, f, 100000) << `\n`;
A expressão de \(\texttt{f}\) foi obtida por manipulação algébrica do seguinte modo:
F(x) = 0 \iff x^2 - cos^2(x) = 0 \iff x^2 = cos^2(x) \iff x = \pm cos(x)Logo no intervalo \([a;b]\), temos que \(x = cos(x)\) ou seja \(f(x) = cos(x)\).
name: 2b class: img-right
2.b)
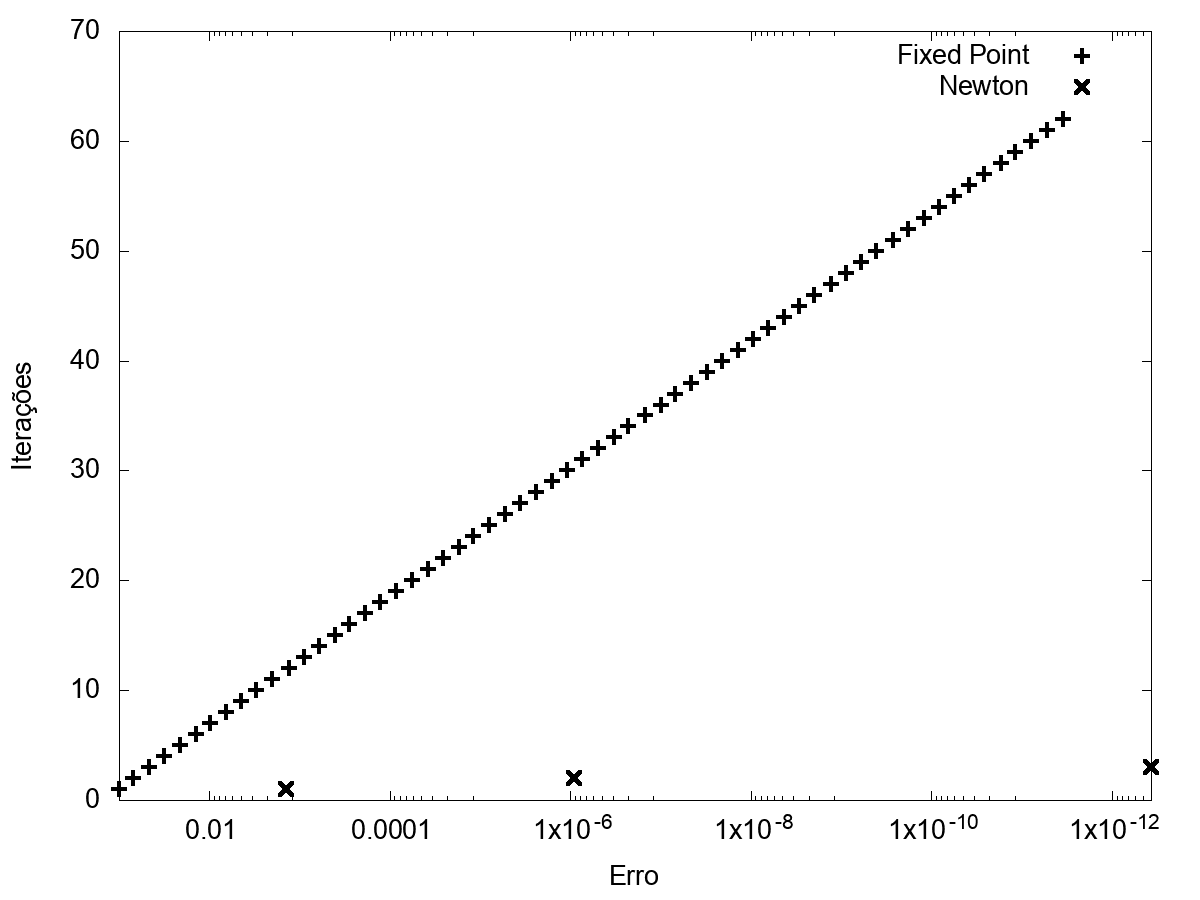
Partindo destes resultados, verificamos empiricameente a diferença na ordem de convergência dos dois métodos.
Obtivemos como valor final para este método o valor \(0.739085133217\), que difere do valor calculado
como o método de Newton em \(-2 \cdot 10^{-12}\), por isso concluimos numericamente que, para os valores iniciais usados, este método pode ser aplicado, sendo que aproxima o valor real.
name: 2b class: img-right
2.b)
Verificando as condições de aplicabilidade deste método, temos que \(f(x)\) é continua em \([a;b]\), verificando-se a primeira condição,
que \(f(0.7) \approx 0.76484219\) e \(f(0.7) \approx 0.69670671\) o que implica que \(f([a;b]) \notin [a;b]\), o implica que não se verifica a segunda condição
e que \(\forall x \in [0.7;0.8] : |-sin(x)| < 1\), o que significa que se verifica a terceira condição.
name: 2b class: img-right
2.b)
Apesar de não se verificar a segunda condição, verificamos na mesma a convergência da sucessão, o que não contradiz os resultados teóricos, uma vez que estas condições são suficientes, mas não necessárias para esta convergência.